Related functions: The coat is not mysterious, first peel open to see
Signal ah signal, I would like to smash you, in fact, it was hacked to death...
What is the signal in the end? For thousands of years, why dozens of ancestors marched in succession, saying that the white is the electromagnetic wave; deeper point is that the shape of the electromagnetic wave contains information; deeper point is that the shape of the electromagnetic wave was coded or encrypted; The bottom line is the electromagnetic wave, but it is just like the carving art. It is rich in "deep meaning", or mellow, or incongruous, or enchanting... [shape please brainstorm]
[I'm sorry, it seems to be pulling away, so the point is coming! 】
What are the related functions? Who came out drops! Why do you do it? This is all you need to think about it!
For example: First, why does the sequence's autocorrelation function show randomness? A series of sequences consisting of +1, -1 is completely random, and the other sequence is completely random - OK. The result of the multiplication must be half -1, half -+1, and all add up must be 0. A completely random sequence, which he got after delaying N beats, must be another completely random sequence. If you agree with the last paragraph, then I do not need to explain it later. If the randomness of the sequence is not sufficient, the +1 and -1 numbers obtained by one-by-one multiplication are not equal, and the result of all the additions is not 0. The worse the randomness, the larger the absolute value of the result.
So what do we see: The correlation function of the signal reveals a secret, how similar I am now to my N years later.
Cross-correlation function
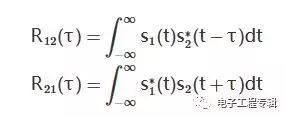
Autocorrelation function
In layman's terms, the nature of the so-called related functions is almost the same as what a person has.
Conjugate symmetry R(τ)=R∗(−τ);
Autocorrelation origin value equal to signal energy R(τ=0)=∫∞−∞s(t)s∗(t−0)dt;
The area of ​​the correlation function equal to the square of the signal area modulus;
F[R(Ï„)] is a real number
If the two signals have the same energy spectrum in the frequency domain and the time domain waveforms are different, the two signals have the same correlation function.
Signal Convolution: Silly Confusion with Related Functions
The preceding related functions have been described. Then what is the convolution? Is it too much trouble? It is not recommended to interpret convolutions such as "reverse/flip/deconvolve/symmetric". Why do good signals need to flip? It is difficult for students to understand the physical meaning of the convolution.
This is actually a very simple concept. Most textbooks in the country are not thoroughly explained.
If you look at the map directly, you don't understand it. For discrete signals, for example, continuous signals are analogous.
Known x[0]=a,x[1]=b,x[2]=c:
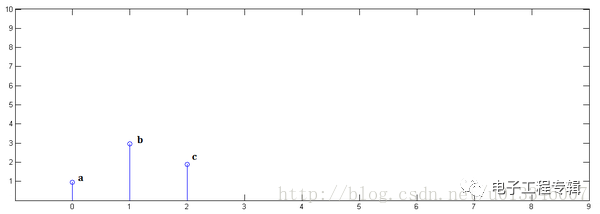
Known y[0]=i,y[1]=j,y[2]=k:
The following shows the process of finding x[n] * y[n] to reveal the physical meaning of the convolution.
In the first step, x[n] is multiplied by y[0] and panned to position 0:
In the second step, x[n] is multiplied by y[1] and panned to position 1:
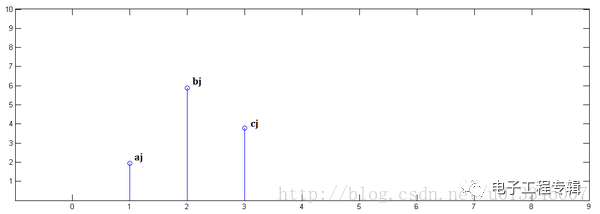
The third step, multiply x[n] by y[2] and pan to position 2:
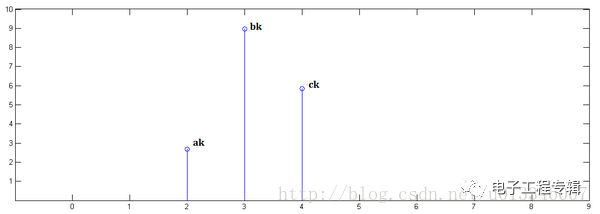
Finally, by superimposing the above three graphs, we get x[n] * y[n]:
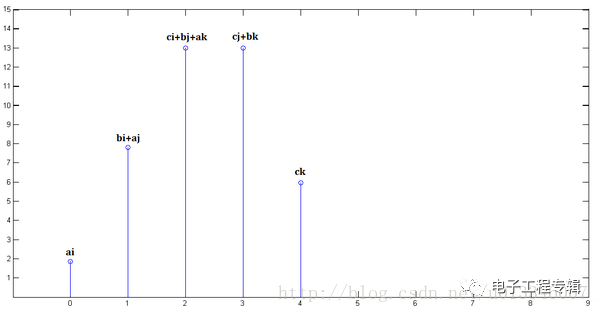
Therefore, the convolution is a weighted summation. In general, a unit response is superimposed on each position of the input signal, and the output signal is obtained. This is why the unit response is so important.
The following move and move, knowing that God is too powerful, have to admire: compound interest of the example to understand the convolution may be better understood:
Xiao Ming deposits 100 yuan and the annual interest rate is 5%. Based on compound interest calculation (the interest will be added to the principal every year to calculate the interest for the next year), then the amount of money he can get after five years is , as shown in the following table: 
After one year of depositing this money in the bank, Xiao Ming deposited another 100 yuan in the bank. The annual interest rate was still 5%. Then the money was calculated on the basis of compound interest. In the fifth year, the amount of money to be recovered was 100(1+5\%)^4, we add this result as a new line to the above table:
And so on, if Xiao Ming deposits a new 100 yuan into the bank every year, then this income form will look like this:
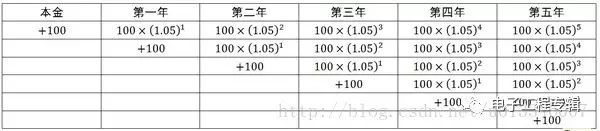
It can be seen that the money eventually received by Xiao Ming will be equal to the sum of the money he got after calculating compound interest from the money he has deposited each year, that is:
Simplifying this formula with the summation sign yields: 
In the above formula, it is the deposit function of Xiao Ming, and the compound interest calculation function of each money deposited into the bank. Here, the money that Xiao Ming finally gets is the convolution of his savings function and the compound interest calculation function.
In order to see this more clearly, we have extended this formula to a continuous situation. That is to say, during the period from this arrival, Xiao Ming deposited money into the bank at all times. His savings function is , And the bank also calculates the income according to the compound formula for each money he deposits, then the total amount of money that Xiao Ming will receive in time is:
This is also the expression of the convolution. The above formula can be written as.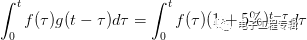 
I believe that through the above example, everyone should be able to clearly remember the convolution formula.
Let's start with two more sentences: If we consider the deposit function of Xiaoming as a process of signal generation (that is, input/incentive), and treat the compound function as a response function of the system to the signal (that is, feedback/response). Then, the convolution of the two can be seen as the observation of the system at a time, and the observations (that is, the output) obtained will be the superposition of all the signals generated in the past after the “processing/response†of the system. This is the physical meaning of the convolution.
Please pay attention to the convolution formula here and compare the related function formulas. You will find interesting things
Input signal: s1(t), impulse response: s2(t)
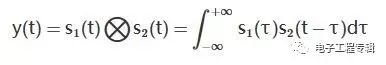
Put the relevant function formula here to facilitate comparison:
Cross-correlation function
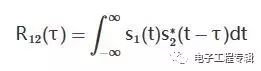
Is it possible to find the point of interesting, get something:
The magic formula: R12(τ)=s1(τ)⨂s∗2(−τ)
What is the nature of the convolution?
Exchangeable/combinable/distributable, remember this
The difference between correlation and convolution
The related formulas and convolution formulas are very similar, and the correlation can use convolutional representations, so some people think that the two concepts are related. In fact, the two are not conceptually related.
The integrand in the correlation operation has no time deconvolution process, and there is a convolution operation.
The correlation function does not satisfy the exchange, and the convolution can.
Functions in Matlab
Cross-correlation (cross-correlation)
Inter-correlation of two discrete time series [The picture did not understand too much. . . 】
Convolution (convolution)
Convolution output of two vectors u, v [picture still not quite understand. . . Again (╯□╰ )】
Simulation analysis
Simulation results
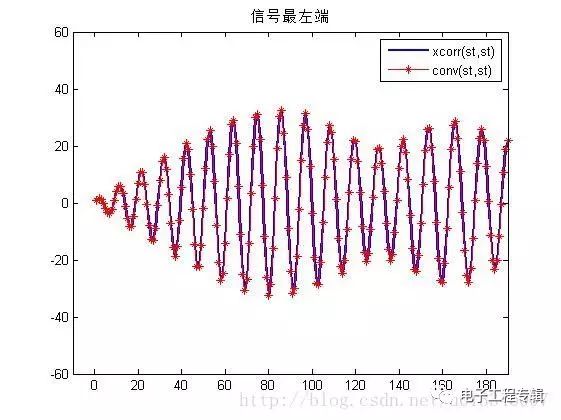
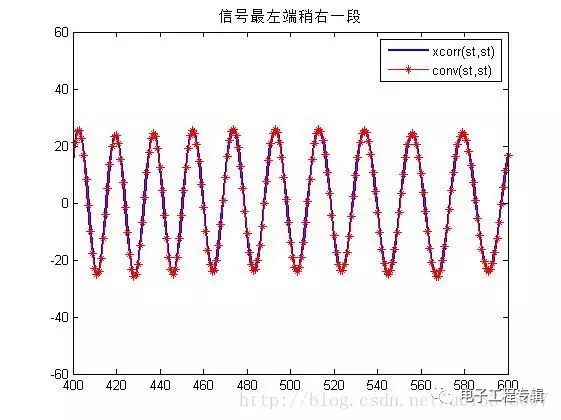
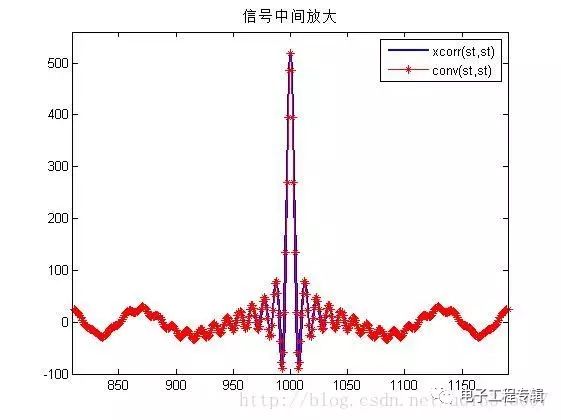
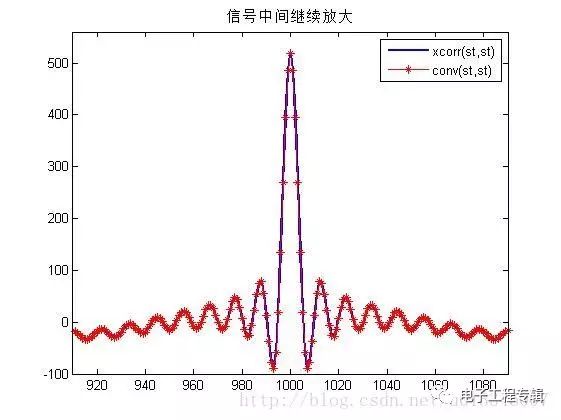
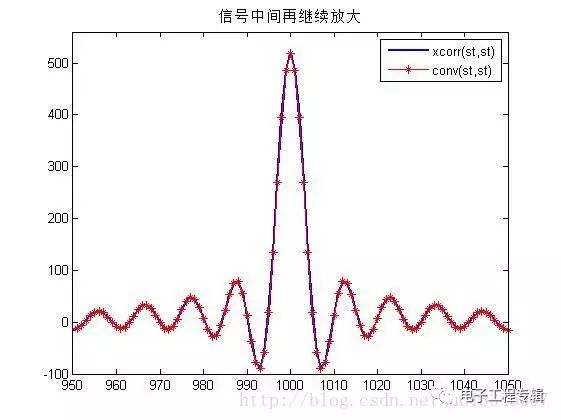
In the above simulation, the autocorrelation function is equal to its convolution with itself! ! Found no! ! ! Meet the point of get! ! ! ! Hahaha R12(τ)=s1(τ)⨂s∗2(−τ)
Ningbo Autrends International Trade Co.,Ltd. , https://www.supermosvape.com